“...The concept of time within present physical theories—by which we mean Newtonian physics, special relativity, and general relativity—is an approximation within a quite different conceptual framework that is associated with a quite different theory.” -J. Butterfield, C.J. Isham, “On the Emergence of Time in Quantum Gravity”
This is the fifth in a series of articles addressing the question “What is time?”
The first dealt with philosophical issues, the second with how we perceive time, the third with entropy as “the arrow of time,” and the fourth with relativistic time. In this post I’ll examine how time in quantum mechanics is strange, but of course, quantum mechanics (QM) in general is strange.(1)
The uncertainty of time in quantum mechanics
You readers probably know about the Heisenberg Uncertainty Principle, particularly as it applies to position and momentum (mass times velocity). Let’s just refresh those ideas. The Uncertainty Principle says that you can’t measure simultaneously and precisely values for both position and momentum of a particle. The uncertainty principle also applies to another pair of variables—time, t, and energy, E:
ΔΕ times Δt not less than [h/(4π)]
ΔΕ is the uncertainty in the measured value of the energy; Δt is the uncertainty in the time at which the measurement is made; h is Planck’s constant. (2)
Here’s an example: fundamental particles—pions and muons—are generated when cosmic rays penetrate the earth’s atmosphere (see here). These particles have very short lifetimes, ranging from less than 10-17s to 10-6s, after which they then decay into more stable particles. During their extremely short lifetime, there will be a “significant uncertainty” in any measurement of mass/energy. This uncertainty relation between energy and lifetime has been verified in a number of experiments (see the link above and here).
Quantum mechanics measurement: past ---> future
Classical physics (that is to say, physics before quantum mechanics) used equations that were time symmetric. That is to say, if time, “t” (as a parameter or coordinate) is replaced by “-t,” the fundamental equations of physics look the same. (3) The replacement of t by -t is equivalent to going backwards in time. The solutions to these equations that corresponded to going backwards in time were almost always discarded as being physically unrealistic (but see below).
This is not the case in conventional, “textbook,” quantum mechanics. If the quantum mechanical state is regarded as a superposition of possible states that could result from a measurement, then the measurement act “collapses” that superposition into one of those component states. (This is the so-called “measurement problem.”) There is past: the superposition of states before the measurement; and there is future: the one state of those possible picked out afterwards by the measurement. This measurement problem is pictorially summarized in the famous Schrodinger Cat paradox.
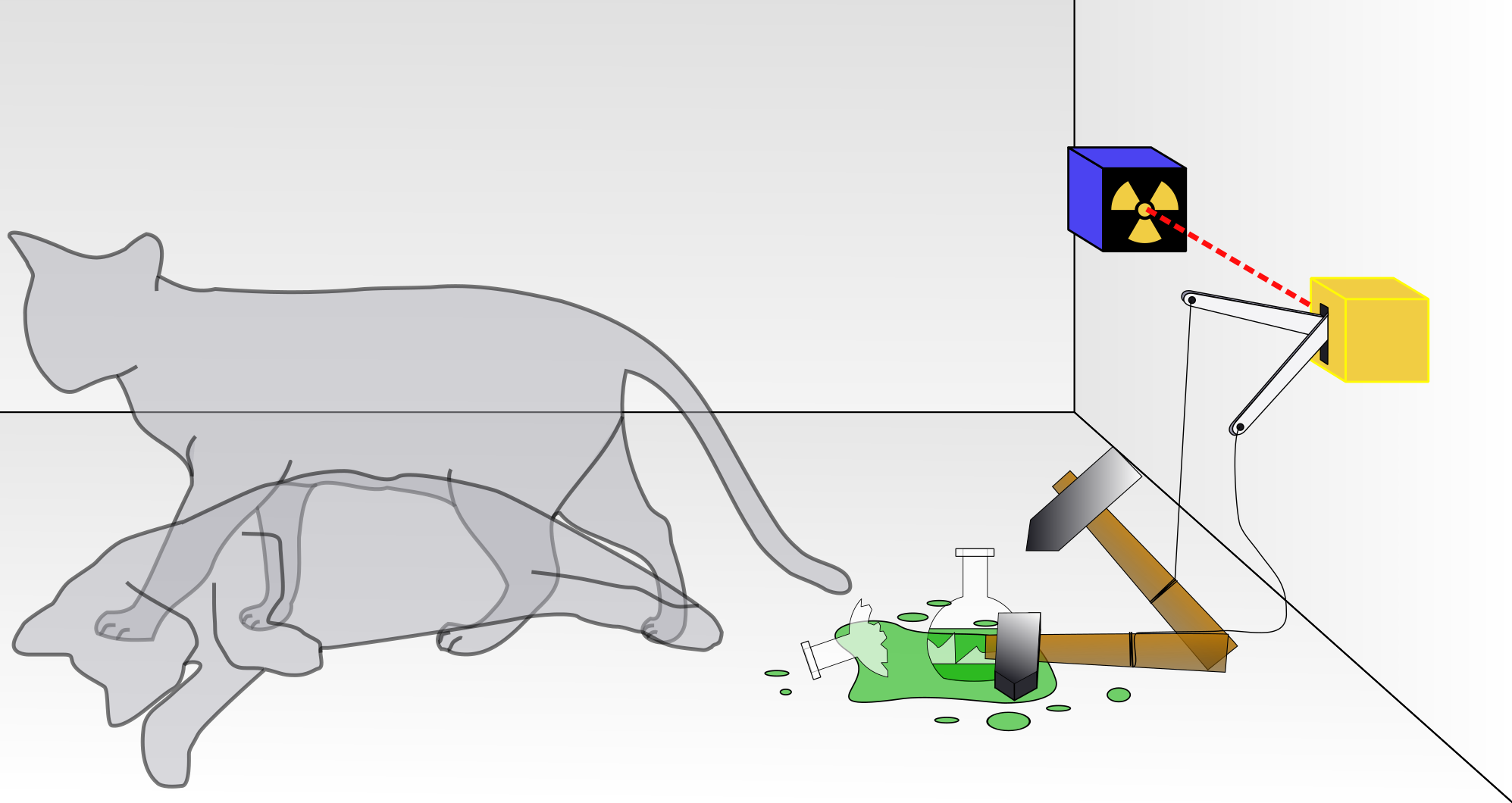 Schrodinger’s Cat Paradox (from Wikimedia Commons). A vial containing cyanic acid can be triggered by a radioactive emitter (purple box). If the radioactive particle is emitted the cat is dead; if not, the cat is alive. Before the box containing cat and apparatus is opened the cat can be regarded as a superposition of live cat + dead cat. After the box is opened (measurement) the cat is either
alive or
dead (not both).
Schrodinger’s Cat Paradox (from Wikimedia Commons). A vial containing cyanic acid can be triggered by a radioactive emitter (purple box). If the radioactive particle is emitted the cat is dead; if not, the cat is alive. Before the box containing cat and apparatus is opened the cat can be regarded as a superposition of live cat + dead cat. After the box is opened (measurement) the cat is either
alive or
dead (not both).
Various QM theories to remove the “measurement problem” have been proposed (see here), but they aren’t universally accepted. Some of these alternatives posit a time symmetry such that events in the future cause events in the present, what is termed “retrocausality.” I’ll examine two of these interpretations below.
Back to the Future with quantum mechanics
From H.G. Wells to Robert Heinlein (4), time travel has been a staple of science-fiction, with the “fiction” part more important than the science. But if some QM interpretations are valid, then time travel—future events influencing the past, retrocausality—is possible, at least for particles on the atomic scale. I’ll focus on one such theory in this section: the Transactional Interpretation of John Cramer. (5)
Before doing that, I want to give one example of backwards time in “conventional” QM. Consider the collision of an electron with its antiparticle, a positron. When the particles meet they are annihilated, releasing two high energy gamma rays (two rays to conserve momentum). The process is summarized in the Feynman diagram shown below:
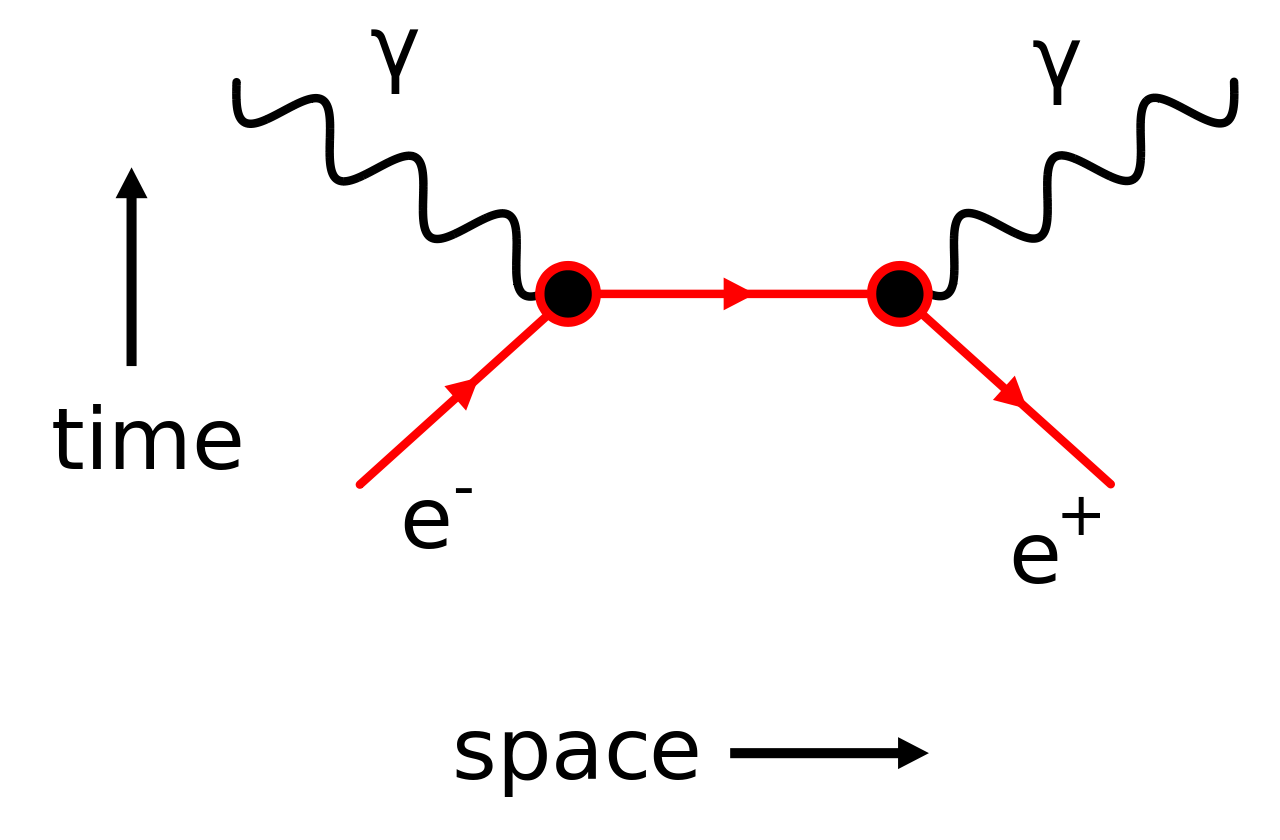 Collision of an electron (e-) and positron (e+) to produce gamma rays (γ), from bitwise via Wikimedia Commons
Collision of an electron (e-) and positron (e+) to produce gamma rays (γ), from bitwise via Wikimedia Commons
Note that the red arrow for the positron is drawn backwards, from present to previous time. This convention represents an “anti-symmetry:” a positron can be thought of as an electron going backwards in time.
The Transactional Interpretation of quantum mechanics: the handshake
“'There's no use trying,' she [Alice] said. 'One can't believe impossible things.' I daresay you haven't had much practice,' said the Queen. 'When I was your age, I always did it for half-an-hour a day. Why, sometimes I've believed as many as six impossible things before breakfast.” Lewis Carroll, “Alice through the Looking Glass”
Quantum Mechanics has several impossible features, but these can be made to seem reasonable by crediting John Cramer’s Transactional Interpretation of quantum mechanics. Some might regard this as replacing several impossible things by one impossible thing, but I’ll let the reader decide that for himself/herself. (5)
Cramer built his Transactional Interpretation on the Feynman-Wheeler absorption theory for electromagnetic radiation (light). (6) He takes the wave-function, a solution to a modified Schrodinger equation, as being real, not just a mathematical device to describe what’s going on. He then takes two solutions to the modified Schrodinger equations, one a wave going forward in time (OW for “offer wave”) and one a wave going backwards in time. The waves, describing some particle or system, meet a measuring device, which then emits another backwards wave (CW for “confirm wave”). The offer and confirm waves engage, that is to say a handshake or transaction occurs, to yield the measurement.
There’s much more to it than the simple description above, but I’ll leave it to the interested reader to follow up by going to the reference given in note 5 and here. This interpretation, like other interpretations of quantum mechanics, cannot be confirmed experimentally. It’s the math, common to all QM interpretations, that is verified empirically, and that has been done for many, many experiments down to 10 figure accuracy.
Quantum mysteries “explained” by the Transactional Interpretation
Here are three “quantum mysteries,” strange behaviors, that the Transactional Interpretation (TI) explains in a common sense way. (By the term “common sense,” I mean that the three strange quantum behaviors listed below are taken into account by one non-common sense hypothesis, interaction with future events.)
- Wheeler’s Delayed Choice Experiment—quantum systems know beforehand if they’re going to be measured;
- Schrodinger’s Cat—the superposition of states and collapse on measurement—a system exists simultaneously in two different states but only one is perceived on measurement;
- The Violation of the Bell Inequality—the nonlocality and instantaneous interaction of coupled particles—separated entangled particles seem to interact instantaneously even though separated by large distances.
Huw Price has given another account (7) of time symmetry and quantum time travel, reasonable on the face of it, which I’ll not discuss here because of space limitations.
Final thoughts
I am not a quantum realist. I believe physics gives a mathematical framework to understand what our world is like, insofar as that may be possible. That is to say, the object of scientific inquiry is to “save the phenomena,” to make coherent and to relate the way things behave. There is a deeper reality, veiled as the physicist/philosopher d’Espagnat would have it, that science does not penetrate. Therefore, I regard theories which treat the future as ontologically real more as conceptual tools to help us picture what quantum mechanics is about, rather than as models for reality.
Now there is one other quantum feature that deals with time: quantum gravity. Again, space limits a discussion of this, so I will just list references for the interested reader. (8,9) Summing these up very briefly: they discuss whether time actually does exist as a fundamental variable, and, if it does, whether like other physical variables that extend over a finite range, it must be discrete, rather than continuous. Indeed, one three body black hole dynamics modeling project suggests that time’s arrow may result from chaotic behavior at the limit of very small discrete spacetime lengths.
What’s to come
In the final article of this series I’ll discuss God, outside of time, and why God created time.
Notes
(1) Here’s one thing to keep in mind: there is a correspondence between a physics equation, as it would be given in “classical” physics and as it is given in quantum mechanics. For example, a vibrating spring models the vibration of atoms in a molecule. The classical differential equation describing such vibrations transforms into an equation with “operators,” the Schrodinger equation. I’ll not go into this in detail, but note only the following: in physics there are pairs of what are called canonical variables: position and momentum, rotation angle and angular momentum, components of angular momentum, time and energy. Heisenberg showed that one could not measure simultaneously and exactly the values for both members of such pairs. This is the Heisenberg Uncertainty Principle. You can get a short, non-mathematical primer on quantum mechanics here. (Pardon the shameless self-promotion!)
(2) Please note that the value of h, Planck’s constant, is so small that uncertainty effects do not manifest themselves for macroscopic objects.
(3) This time symmetry is followed for conservative systems. For situations where there is transport (flow of matter or energy) or dissipation (e.g. friction) then time will have a direction. The time dependent Schrodinger equation (which includes a partial derivative of the wave-function with respect to t, time) is not symmetric in time.
(4) Heinlein gave perhaps the most ingenious twist to time travel with the story, “—All You Zombies—” (WARNING: SPOILER!) in which a man became his own mother and father.
(5) Ruth Kastner has written a fine book for the non-scientist about Cramer’s Transactional Interpretation. For those with a stronger physics background, Cramer’s review articles (here and here) give an excellent exposition of his arguments.
(6) In that theory both “advanced” and “retarded” waves are used as vehicles for radiation emission and absorption. The advanced waves go backwards in time; the retarded waves go forward in time; both are solutions of the wave equation for electromagnetic radiation. Conventionally, advanced wave solutions are discarded as physically unrealistic.
(7) See here.
(8) Isham and Butterfield have written an interesting article on how time might emerge from a theory of quantum gravity.
(9) Carlo Rovelli discusses time in all its aspects--philosophical, relativistic, thermodynamic (“Time’s Arrow”), psychological, quantum gravity--in a fine book, “The Order of Time.” He concludes that time is an illusion, a psychological mechanism brought about by evolution. It’s a fine book, even though I disagree strongly with his conclusion.
Read Also:
What is Time? Part I—Philosophy

