Does Quantum Mechanics Speak to Theology?

“I think I can safely say that nobody understands quantum mechanics.”
—Richard Feynman, Nobel Prize winner for his research on quantum electrodynamics

Seventy years ago, when I first heard this quote (auditing Feynman’s Caltech graduate course on quantum mechanics), I thought, “What does he mean by that?” Now, after a lifetime of research and teaching involving quantum mechanics, I get the picture. The mathematical formalism of QM (quantum mechanics) accurately predicts the results of atomic and sub-atomic experiments. But how we interpret QM, the picture of reality given by those experiments, is clouded and mysterious. 

ChatGPT gives seven interpretations for QM. If you search Wikipedia for “quantum mechanics interpretations,” you’ll find a list of 16 principal ideas. And that list doesn’t include one that is most satisfying to the believing Christian, one that proceeds from Aristotlean and Thomistic principles. (I’ll discuss this interpretation at some length below.) Since each of these interpretations is consistent with the mathematical formalism of QM, it cannot be excluded empirically since the formalism has yet to be contradicted by any experiment.

Why are there so many different ways to try to understand QM? Because the behavior of atomic and subatomic systems in QM experiments is strange and counterintuitive. I’ll try to give a simple picture of these strange behaviors, “mysteries.” But before I do that, let me set forth some basic QM concepts. For a more detailed pictorial and non-mathematical explanation, the reader can refer to this webinar and this ebook.

BASIC QM CONCEPTS

1. The Wave-Particle Duality

The best way to appreciate this concept is to see how it developed, that is, to use a historical perspective (see here). However, to keep this article short, I’ll just state the results from 27 years of research in the early 20th century.

Light, heat, x-rays, microwaves, and radio waves are electromagnetic radiation. Classical physics (before QM) described electromagnetic radiation as waves. Waves (as in waves in the ocean) extend indefinitely; they are not localized, and they don’t have a specific location corresponding to some point in space. If you pass a ray of light through a hole, it can spread out from the hole; that is, the ray can bend around a corner. But QM showed that radiation could also behave like a particle; Einstein’s explanation of the photo-electric effect presumed that light consisted of particles (photons) with energy given by the frequency of the light rays; the greater the frequency (the shorter the wavelength), the greater the energy of a photon. 

According to classical physics, electrons, protons, atoms, etc., were to be treated as particles, which have a specific location as a point in space. In 1924, Count DeBroglie, proceeding from considerations of special relativity, postulated that particles could behave like waves. His prediction was confirmed in 1927 by the Davisson-Germer experiments. 

Here are some pictorial representations of this behavior:

Waves Behaving Like Particles: The Compton Experiment:

In this experiment (Arthur Compton, 1923), a photon collides with an electron at rest and bounces off, moving the electron. Conservation of momentum relates wavelengths of incident photon to that of the scattered photon and the directions of photon and electron after collision, as shown in the diagram below (conservation of momentum means that the total momentum of the scattered photon and moved electron equals the momentum of the incident photon; don’t worry about the math).

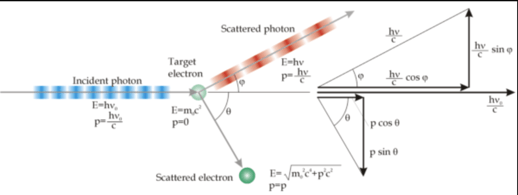Compton Scattering: Astarte.Mauro / Public domain via Wikimedia Commons Compton received the Nobel Prize in 1927 for this work.

Particles behaving like waves: the Double Slit diffraction experiment

Richard Feynman used this experiment to introduce students to QM. It illustrates the strange, wavelike, non-classical behavior that electrons and other atomic and sub-atomic entities can display (entities that we ordinarily think of as particles). First, note that light can bend around corners, which show diffraction properties, as shown in the image below:

Diffraction of Light

Lookangmany thanks to Fu-Kwun Hwang and author of Easy Java Simulation = Francisco Esquembre / CC BY-SA 3.0 via Wikimedia Commons. The green stripes represent peaks in the electromagnetic wave (light); the wavefront goes from a plane wave (up and down green stripes) before encountering the slit (the hole in the yellow line representing the screen) to a circular wave (circle green stripes) after it goes through the slit. Note that any wave has a maximum in the disturbance and a minimum (represented as negative) and a zero disturbance between the maximum and minimum.

Now let’s consider light going through two slits, as shown in the image at the right. The single wave is divided into two waves by the slits. Each of these two waves has a maximum (positive) and a minimum (negative) as in the diagram above, except that the maxima of the wave going through the upper slit is displaced from the maxima of the wave going through the lower slit because of the separation of slits. When the maxima or minima of the waves coincide, an increase in intensity will be observed on a viewing screen. When the maximum of one wave (positive) coincides with the minimum of the other wave (negative), the two disturbances will cancel out, and there will be zero intensity. Thus, the pattern on the viewing screen will be a series of bright bands and dark bands.

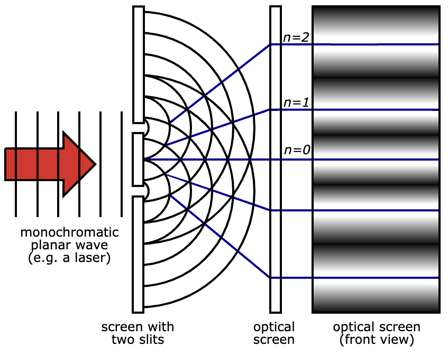Two-Slit Experiment Light Inductive Load / Public domain via Wikimedia Commons

When a particle goes encounters the two slits, it behaves like a wave until it hits the detecting screen; it doesn’t spread out on the screen but lands in a particular spot. After many particles go through the two slits, the pattern on the detecting screen resembles that of waves but with discrete points where each particle has hit the screen, as shown in the diagram below.

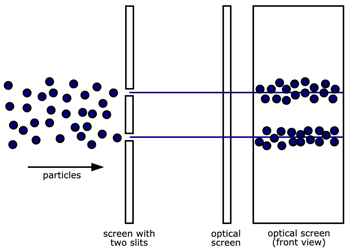Classic Physics: Two-Slit Experiment Particles inductive load / Public domain via Wikimedia Commons

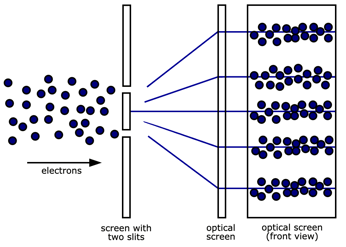Quantum Physics: Two-Slit Experiment Electrons inductive load / Public domain via Wikimedia Commons

According to classical physics (top graphic), the particles would pass through the slits in a straight line, as shown in the left-hand picture. Quantum physics (lower graphic) says the particles behave as if they were a wave after they have passed through the slits but become particles (that is, localized) when they hit the detecting screen.

Let’s turn now to the second strange quantum behavior, entanglement.

2. Entanglement

Any reader of science fiction knows that faster-than-light communication is possible—look at all the stories that make use of it. However, relativity theory says that no information and no forces can act at faster-than-light speeds. But, if we look at the quantum mechanical behavior of pairs of particles (photons, electrons) produced in special ways, the properties of each of the pairs are correlated. This correlation persists even when the pairs are separated over a long distance, so one could think of this correlation of properties as an instantaneous interaction, acting at faster-than-light speeds. Einstein called this behavior “spooky action at a distance.” It was one of the reasons he didn’t think quantum mechanics supplied a complete picture of how the universe works.

Let's use a non-physics example to get a more intuitive picture of what quantum entanglement is about. (To do it as physics would require too much background material for this brief article.) Consider the voting habits of a married couple, husband (symbolized by H) and wife (symbolized by W). Each can vote Democratic (symbolized by D) or Republican (symbolized by R). We’ll suppose the couple is harmonious politically so that one could have either (HR, WR) or (HD, WD); that is, the husband and wife both vote the same. Now, the notion of entanglement is that even if the husband and wife have been separate for a period of time and over a long distance—in a distant future, the husband on Earth and the wife on Mars or even separated by light years—the husband and wife will vote the same at the same instant in time, their vote will always be either (HR, WR) or (HD, WD).

Entanglement has been experimentally verified, and it holds even for particles of a pair separated by many miles. Shown below is an illustration of one such experiment.

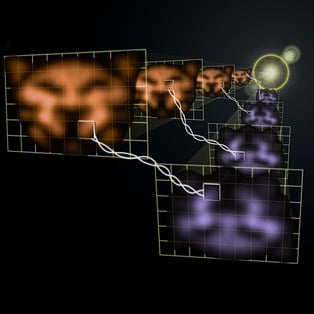National Institute of Standards and Technology / Public domain via Wikimedia Commons. The pictures are images of the face of a cat transmitted by two laser beams; the photons in each beam are entangled. Since the photons are entangled, as each beam travels and becomes separated, the fluctuations in intensity (shown as little squares) are the same for corresponding parts of the image. (Note that the purple face is upside down with respect to the orange; see here for a more complete account.)

Let’s turn now to how these strange quantum behaviors might be interpreted theologically.

QM INTERPRETED: BACK TO ARISTOTLE AND AQUINAS

“The one thing worse than a theology that attempts to draw connections between physics and God is a theology that believes it has no need of such connections, a theology that believes it can concoct the divine out of metaphysical whole cloth.” —Philip Clayton, “Tracing the Lines,” in Quantum Mechanics: Scientific Perspectives on Divine Action.

Theologians, philosophers, and physicists give different answers to the question, “Does quantum mechanics speak to theology.” Rather than discussing these positions here, I refer the reader to my ebook, Mysteries: Quantum and Theological. In this article, I focus on a newer way to look at QM, using concepts from Aristotelian and Thomistic metaphysics. Since I cannot, in this brief piece, give a detailed explanation of these concepts, I’ll give references to internet resources that give fuller accounts and ask the reader to pardon my physics accent in speaking philosophy.

Aristotelian/Thomistic Metaphysics for Dummies (Me)

Readers who are familiar with Aristotlean/Thomistic metaphysics can skip this section. Those who are not and want to get a fuller account can refer to YouTube explanations of the various terms or read Gil Sander's article, An Aristotelian Approach to Quantum Mechanics, which gives a clear definition of relevant terms.

Let’s look at the following example of a “thing” changing (thing (agent of change) —> changed thing):

Ice cube (add heat) —> liquid water (add salt, electrolyze) —> H2 and O2 gases (much heat) —> H and O atoms

Now the ice cube is a substance, having matter and form; it has properties—shape, transparency, hardness (“accidents”); it is in existence (“actus”); it can be changed by an external agent (e.g., heat) into something different, liquid water, so it has the potency (“potentia”) for transformation. We could proceed with further transformations and change the H and O atoms into electrons and nuclei (protons and O¹⁶ nuclei) and, further yet, transform the O¹⁶ nuclei into neutrons and protons. 

At each stage in this series of changes, the “thing” is composed of what Aristotle would call “matter,” and the “thing” has a “form.” It’s apparent that the changes certainly involve changes of form. Whether there is a change of “substance” (as understood in an Aristotelian context) is perhaps more difficult to say. I would say that each of the changes involves a change in substance. However, when the question is asked of AI agents (ChatGPT or Bing CoPilot), one gets different answers. The kind of matter that is present is certainly different in each stage. What is relevant to this article is that there is the possibility of change (“potentia”) from one actual state of being (“actus”) to another.

This last condition is the most relevant one in explaining QM strangeness, and this explanation is what we will discuss now.

Heisenberg invokes Quantum Potentia

In his book about physics and philosophy, Werner Heisenberg, a pioneer in establishing quantum theory, turned to Aristotle to explain some of the QM mysteries. He attributed the probabilistic nature of a quantum measurement to the Aristotelian concept, “potentia”:

“One might perhaps call it an objective tendency or possibility, a “potentia” in the sense of Aristotelian philosophy.”—Werner Heisenberg, Physics and Philosophy: The Revolution in Modern Science, (1958)

Building on Heisenberg’s interpretation, several philosophers have developed a complete interpretation of quantum theory based on Aristotelian/Thomistic concepts (see References). I’ll summarize these ideas below.

Aristotelian Quantum Mechanics

As this physicist sees it, philosophers have taken two approaches in using Aristotelian/Thomistic metaphysics to explain QM. The first is to incorporate it as a whole; the second is to focus on the concepts of potentia (potency, possibility) and actus (real, actual) as describing reality. The latter approach is taken by Kastner, Kauffman and Epperson (KKE), which I’ll discuss below.

KKE uses the terms res potentia and res extensa to describe the nature of a thing (“res”). That which is a res extensa is real and can be perceived directly by sense or measuring instruments; that which is a res potentia is also real but cannot be perceived directly by sense or measuring instruments. According to KKE, measurement can convert a res potentia to a res extensa, as in the two-slit experiment:

Consider the following two propositions concerning a two-slit experiment:
‘The photon possibly went through slit A.’ Note that one can say of X: ‘X is true AND ‘not X’ is true’ without contradiction. Thus X, understood as a statement of possibility, does not obey the law of the excluded middle. On the other hand, consider Y: The photon was detected at point P on the detection screen.’ Y, as a statement about an actuality, does obey the law of the excluded middle.”
—KKE, Taking Heisenberg’s Potentia Seriously.

Proposition X implicitly considers the incident photon as a wave extended over space, which is to say the photon can be at both slits and unless a measurement occurs just after it passes through the slits, it is still extended in space. If the photon is measured just after it passes through the slits potentia is changed to actus, and the photon acts as a particle that is localized at a point. Proposition Y implicitly considers the photon detected at a point on the screen to be a particle. Thus, the measurement (photon hitting the screen) in some way converts potentia to actus, or res potentia to res extensa. And the same process occurs in the macroscopic world, according to Aristotle: an external agent of sufficient power can convert the potentia of a substance into actus (e.g., electrolysis can convert liquid water into H₂ and O₂ gases). 

KKE explains entanglement by supposing that the act of measurement removes all but one of the possible entangled states so that only the measured one remains. We can look at this way, using the example above of an entangled husband/wife pair that votes the same way. Let’s take the quantum state before measurement to be (husband, D; wife, D) + (husband, R; wife, R), which is equally likely beforehand for the couple to vote Democrat or to vote Republican. Then measurement—voting—will leave either (husband, D; wife, D) or (husband, R; wife, R). This will be the case whether the husband and wife are separated by 1 meter or by a light-year. KKE concludes that this description of multiple actualities is a reality, albeit only a possibility (that is, existing as quantum potentia), and that such entanglement is independent of space-time restrictions.

If you ask, “Is anything added to our knowledge of what quantum mechanics is all about by such an Aristotelian/Thomistic interpretation?” I would answer yes if you take that interpretation to describe how the universe works generally. Since this short article is only an amuse-bouche for understanding QM via Aristotelian/Thomistic metaphysics, I recommend the reader go to the References listed below for the full meal.

REFERENCES

1. Alfred Driessen, Aristotle and the Foundation of Quantum Mechanics
2. Gregg Jaeger, Quantum Potentiality Revisited (a complete explanation of how quantum theory can be put into an Aristotelian/Thomistic metaphysical frame)
3. R.E. Kastner, Stuart Kauffman, Michael Epperson, Taking Heisenberg’s Potentia Seriously
4. Robert Koons, Knowing Nature: Aristotle, God and the Quantum; Thermal Substances: a Neo-Aristotelian Ontology of the Quantum World
5. Gil Sanders, An Aristotelian Approach to Quantum Mechanics (an excellent, intelligible explanation of Aristotelian metaphysics and its application to understanding QM)
6. Guiseppe Tanzelli-Nitti, Thomism, Nature and Science

 **Previously published on “Matt Briggs, Statistician to the Stars” blog. Republished with permission.