“‘Contrariwise,’ continued Tweedledee,‘if it was so, it might be; and if it were so, it would be; but as it isn’t, it ain’t. That’s logic.’”—Lewis Carroll, Through the Looking-Glass
How exactly do we know what we know or come to believe what we believe (other than faith or revelation)? One explanation is by employing rational inquiry. Linguist Noem Chomsky writes that through rational inquiry we “discover crucial features of the world.” This discovery comes through what we already believe to be true and what we observe:
“Data and observations, in the sciences, have an instrumental character. They are of no particular interest in themselves, but only insofar as they constitute evidence that permits one to determine fundamental features of the real world . . . ” — Noam Chomsky, New Horizons in the Study of Language and Mind
With rational inquiry, there are 4 basic ways to proceed:
- Deductive logic
- Induction or inductive reasoning
- Abductive reasoning (reasoning to the best explanation)
- Retroductive reasoning (reasoning based on models)
We will discuss each in turn.
1. Deductive Logic
Deductive logic draws conclusions from propositions we believe to be true (“premises”) using logical procedures that were first set up by Aristotle (going from the general to the specific). We will look at deductive logic in three parts: syllogisms and Venn diagrams, sorites, and logical paradoxes.
Syllogisms and Venn Diagrams
One example of deductive logic is a syllogism, in which you come to a conclusion based on two propositions. The following Gelett Burgess poem is a syllogism (brackets are mine):
All cows are purple. [Major Premise]
This animal is a cow. [Minor Premise]
This animal is purple. [Conclusion]
If you know the premises to be true, then the conclusion is true. If the premises aren’t generally true (as in this example), then the conclusion may or may not be true. For example, you could paint a cow purple, or it could be a mutation.
Note that the word “all” before cows is an important qualifier. Changing the word “all” with "some" or "no" changes the meaning, as illustrated in the Venn diagram below:
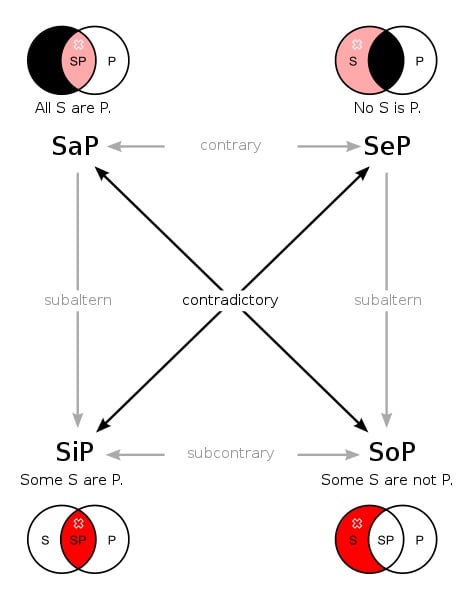Venn Diagrams to Understand Logic: The Rule of Opposition.
Black Areas: area is empty
Red Areas: at least one element in area
Faded Red: non-empty areas.
From Wikimedia Commons
Sorites
Oxford academic Charles Dodgson (better known as Lewis Carroll, author of the Alice books), gave us many amusing and complicated puzzles that mixed his love of nonsense and logic. These polysyllogisms are termed sorites. Some of Carroll’s logical puzzles were exceedingly complicated, involving many statements and logical variables. Here’s a relatively simple one:
- All babies are illogical.
- Nobody is despised who can manage a crocodile.
- Illogical persons are despised.
We combine 1 and 3 to give:
- All babies are despised.
Then 4 and the contrapositive of 2 can be combined to yield:
- No baby can manage a crocodile.
More complicated polysyllogisms may require computer methods for their solution! Since some of the statements may be redundant or contradictory, logicians use a special type of analysis—a subdiscipline of mathematical logic called the "satisfiability theory."
One might be tempted to conclude that the deductive method should yield propositions that are either true or false. Not so! There are uncertainties—paradoxes—in logical deduction, which is the topic we’ll look at next.
Logical Paradoxes
“A paradox, a paradox, a most ingenious paradox!” –Gilbert & Sullivan, The Pirates of Penzance
Can deductive logic always yield an unambiguous true or false set of propositions? In his very fine book, Labyrinths of Reason, William Poundstone gives examples of logical paradoxes for which it is difficult to make a true judgment. Perhaps the most famous of these is the Cretan Liar paradox (see Star Trek, Fooling the Androids Episode):
Epimenides the Cretan says, “All Cretans are liars.”
Question: Is this statement true or false? If it is true, then Epimenides is a liar, but if Epimenides is a liar, how can his statement be true?
There is also the barber paradox:
A barber is a man in town who shaves all those, and only those, men in town who do not shave themselves.
Question: Who shaves the barber? If the barber doesn’t shave himself, according to the statement he does shave himself…
Both paradoxes invoke self-reference—hence the paradox. Bertrand Russell attempted to deal with the problem of self-reference by his “Theory of Types,” which sets up a hierarchy of statements, i.e., statements about statements, statements about (statements about statements), etc.
Next, we’ll move on to another rational path: induction or inductive reasoning. The results aren’t as sure, but it still is a basic route to judgment in law, science, and everyday life.
2. Inductive Reasoning
“The deductive method is the mode of using knowledge, and the inductive method the mode of acquiring it.” —Henry Mayhew, 19th century British Journalist
Induction is generally regarded as proceeding from particular instances or events to a general conclusion. (I’m not referring in this context to the mathematical method of proof.) Here’s an example:
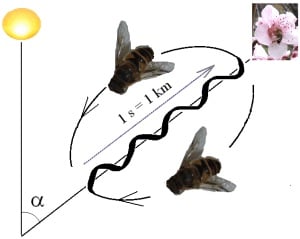
Bee Waggle Dance
Distance—How long the waggles occur gives the distance of the flowers.
Direction—Where the bee points show the direction.
from Wikimedia Commons
A naturalist named Karl von Frisch noticed that bees move their rear end back and forth in a special way (or “dance”) after they have been gathering nectar from a certain group of flowers. The dance is the same for a given group of flowers. Because he concluded that this bee-dancing is a communication to other bees about the location of the flowers, von Frisch received a Nobel Prize. (However, we’ll see below that science is generally more than collecting data and making inferences. Until then, here’s a neat video of bees doing the waggle dance).
Note that there are also methods of assessing inductive reasoning propositions by means of probability statements, the strength of belief quantification, and Bayesian probability analysis. See “The Problem of Induction” in the Stanford Encyclopedia for more on this.
Next, we shall discuss abductive reasoning, that is, reasoning to the best explanation.
3. Abductive Reasoning—Inference to the Best Explanation (IBE)
“When you have eliminated the impossible, whatever remains, however improbable, must be the truth.” —Sherlock Holmes, The Sign of the Four
One of the best-known examples of abductive reasoning is given in the quotation above and indicated by its commonly used name, “Inference to the Best Explanation” or “IBE.” IBE uses given data to infer the most likely explanation of a past event that could have caused the data. It is commonly used in the so-called “historical sciences” (geology, paleontology, and cosmology) for which laboratory experiments aren’t in order.
Here’s an everyday example adapted from one given in Stephen Meyer’s book about Intelligent Design, The Signature in the Cell:
You look out your window and note that your driveway is wet; three possible explanations occur to you: it has rained, the sprinkler has been set so that it also wets the driveway, your car has been washed. You notice that neither the street nor your lawn is wet, so you conclude that the third explanation—your car has been washed—is the correct one. A pail of water beside your car is confirmatory evidence for that conclusion.
Some philosophers of science claim that IBE lacks certainty and leads to false conclusions. In the past, theories proposed as best explanations have turned out to be duds: phlogiston as caloric fluid for heat, either as a medium for electromagnetic waves, etc. However, it should be kept in mind that these theories were disproved by additional empirical evidence (caloric theory of heat by Count Rumford’s cannon-boring experiments; and the ether as a medium for electromagnetic waves by the Michelson-Morley experiments).
Finally, let us turn to retroductive reasoning.
4. Retroductive Reasoning
“In a retroduction, the scientist proposes a model whose properties allow it to account for the phenomena singled out for explanation. Appraisal of the model is a complex affair, involving criteria such as coherence and fertility, as well as adequacy in accounting for the data. The theoretical constructs employed in the model may be of a kind already familiar (such as ‘mountain’ and ‘sea’ in Galileo’s moon model,) or they may be created by the scientist specifically for the case at hand (such as ‘galaxy,’ ‘gene,’ or ‘molecule).” —Ernan McMullin, A Case for Scientific Realism
Retroductive reasoning is commonly used by scientists to explain phenomena by a familiar model. A very early example is that in which Galileo explained the differing patterns of light and dark on the moon at different orientations with respect to the sun. He proposed that the moon has seas and mountains on it, just as the earth does.
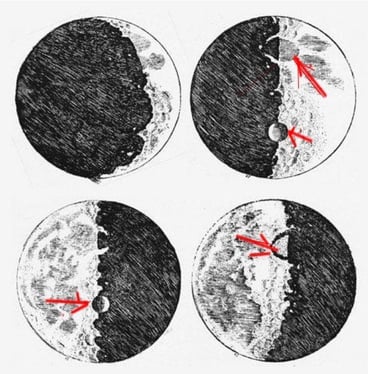Galileo’s Moon Sketches: Red arrows show different shadows and light, depending on the direction of sunlight; these light and shadow patterns suggest the presence of mountains and craters. Modified from Wikimedia Commons
Another example of retroductive reasoning comes from contemporary molecular physics. It is the model used to describe molecular vibrations (nuclei in a molecule vibrating back and forth): a weight attached to a spring, vibrating back and forth—the so-called “harmonic oscillator.”
|
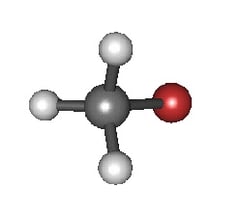
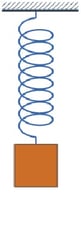
Model for vibrating molecules: |
Conclusion
In this article, I have shown (I hope) that rational inquiry has limitations. Deductive logic is not complete, since there are paradoxes with which it cannot deal. Inductive, abductive and retroductive reasoning help us to understand, but they do not yield absolute truths.
Science, which employs these modes of rational inquiry, requires both theory and reproducible empirical validation. We’ll see in the next article why science does not give us eternal truths; rather the “truths” of science change as new data and new theories come into play.
Note: These articles are adapted from my Web-book, “Truth Cannot Contradict Truth.”
